やっと最終解にまで到達した 「 大ピラミッドを建造するいちばん簡単な方法 」 の総まとめ ジャン・ピエール・ウーダン氏の 「 内部らせん斜路 」 仮説を発端にして ) やっと最終解にまで到達した 「 大ピラミッドを建造するいちばん簡単な方法 」 の総まとめ Copyright　2018.3.8.　by　うつぎれい 　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　 ( アイディア )　( 2018.2.18. 〜 3.8. 記 ) 余りにも何度も紆余曲折して最終結論にと至った元ページの本論は、それ自体が解明過程そのままの記録として捨てがたいものの簡潔性には欠けてるので、此処にその発端としての 「 ウーダン説 」 と、最終結論となった自説 「 外壁斜面切り通し螺旋斜路 」 ＋ 「 クレードルと足の生えた錘 ( 人間の体重 ) と循環型縄梯子ヤグラの徹底的な活用 」 ＋ 「 石灰岩 ＝ 古代コンクリート 」 …の要点のみを改めて ( 脱線せずに ) 書き纏めておきたい。 ウーダン氏の 「 内部らせん斜路 」 仮説が従前の説より抜きん出て優れていた点は、完成時に斜路の全体がそのままピラミッド本体に組み込まれ、( ピラミッド外部の 「 直線斜路 」 や 「 外に張り出して巻き付く建設用仮設斜路 」 とは異なり ) 撤去の必要が全く無く、その建設作業の一切が無駄にならない …という点であった。 が、ウーダン説は奇妙にも、建設の途中まではピラミッド外部の巾広直線斜路を使い、そこから上の建設のみトンネル型の内部らせん斜路を使っての建設 …という折衷案になっていた。 　( 2018.3.27. 追記 ; 改めて説明映像を見直してみたら、高さ ６０ メートルまで使う外部直線斜路はその後解体し、その石を再び内部らせん斜路で運び上げて本体建造に再利用する …という、何と ３ 重の折衷案になっていた。 　　恐らく １ / ３ の高さまでの外部直線斜路を造る為の石の数が、其処より上のピラミッド本体を形成する為の石の数とほぼ同じ、…と算定しての ３ 重折衷案なのだろう。 　　が、ウーダン氏はその解体撤去 ・再利用プロセスでの、「 工事作業と労力の余りの無駄さ 」 にはまるで気付いていないように見える。 ) 　[ ウーダン氏の提示している下の説明図を詳しく見てみると、実は他にも色々と不思議な点が見付かる。 例えば下の図で ( 一見すると切り通し型に見える ) 人員回送用のテラス は 張り出し型 斜路 のようにも見え、凡そ ２ メートル以上も外壁から外に突き出てる。 これだと 「 外側に何もハミ出さない内部斜路ゆえに測量が正確に行えてピラミッドに歪みが生じない 」 という当初の主張利点がまるで無くなってしまう …のではないだろうか？　そしてもしこのような人員回送用テラスが実際に造られ、使用されてたのだとすると、ピラミッド建造の終盤では、それ程にも高さのある切り通し空間をすべて 「 巨石と化粧石とで完全に埋め尽くさなければならない 」 と共にその人員回送用のテラスをも完全に解体撤去せざるを得ないのだが、回送用テラスは斜路でなく、巨石は内部トンネルで運び上げられ、カドの開口部からしか外に運び出せないのなら、一体どうやって ( 開口部から遠い ) テラスの改修個所にまで運ぶことが出来たのか？ ( テラスを解体した石を当の空間に積み上げたのだろうか？ )　また、回送用テラス解体撤去工事以降の 「 人員の回送 」 は一体どうしていたのだろう？　更に「 カド部での方向転換 」 を含めての 「 巨石運搬用ソリそのものの回送 」 は果たしてどうやって実現していたのか？ 等々である。 ] 　　　　 これらの画像はウーダン氏と DASSAULT SYSTEMS の製作映像からの引用である。 これは恐らく 「 玄室 」 周りの花崗岩巨石の運び上げには、巾 ２.２ メートルの内部斜路では無理 …という判断からの折衷案採用であったと思われたが、いささか不思議であった。 というのは、「 建設の途中までは 〜 直線斜路を使い 」 というウーダン氏の上の言葉は、どう考えても上の図での 「 トンネル入口までの直線斜路 」 を指してる筈が無いからだった。 それはむしろ、この下の図での 「 唯々、玄室天井用の花崗岩巨石を運び上げる為にだけ使われる、大回廊と一対になって殆ど同じ傾斜角でピラミッド本体にも食い込んでる 」 方の、「 急峻な直線斜路 」 を指してこそ、そう言ってるのに違いなかったからである。 そうでないと意味が全然通らない。 　( 実は私もたった今、その意味でしか有り得ない事に漸く気付いたばっかりである。 ) なぜなら、平均 ６０ トンの花崗岩巨石の運び上げについて、ウーダン説では 「 大回廊 」 に巨大な錘石？をいわゆるエレベーターの 「 バランス錘 」 のように設置し、運び上げる花崗岩の重さをそれで相殺することで、( 系全体の慣性質量にだけ対峙する ) 比較的小さな力？ で運び上げられる …と考えているからである。　( この下の各々の図を参照のこと。 ) つまり、だからこそ大回廊と対になる ( 折角の ４ 度勾配をまるで無視した ) 急傾斜の直線斜路なんていう、何ともチグハグな発想 …になってしまったのだろう。 やれやれ …、漸くウーダン説のトンデモない真相が分かって来た。 まさかそんな事だとは、思ってもみなかった！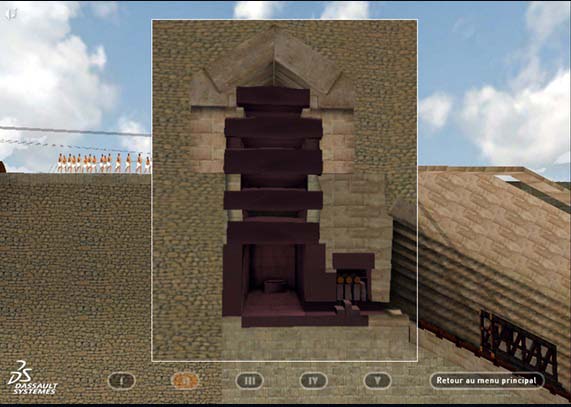 　　 これらの画像はウーダン氏と DASSAULT SYSTEMS の製作映像からの引用である。 処で、ウーダン説でとりわけ重要だったものの一つは、実は、ピラミッド外壁斜面に残る微かな痕跡からウーダン氏が斜路の勾配を ４ 度 …と見抜いてそれを断言して呉れたことであった。 　　　　 そのお陰で以後、多くの具体的な計算が、私にも可能になった。 　( そうでなければ、私は、何も考え始めなかったかも知れない。 ) そして実はこの 「 外壁斜面に残る微かな痕跡 」 には大きな意味があった …と後に判明したのである。 さて、その一方でウーダン説には、それ以前から知られていたピラミッドに関する基本的な事実について、重大な見落としが実は幾つもあった。 ● ピラミッド低層段の奥には 「 石灰岩の低い岩山が埋もれて 」 おり、ピラミッドはそれを覆って建てられてること ピラミッド基壇など低層段に於いて、石積みによって形成されてるのは周縁部分についてのみであり、低層段外周の直ぐ奥には石灰岩の低い岩山がそのまま鎮座している。 ピラミッドはそれを直方体の石で覆って土台とし、その上にこそ造られたものであること。 　( これを最初に解明したのはアメリカの考古学者 マーク・レーナー 氏である。 ) 　　　　　　　　　　　　 ● 花崗岩巨石を除く殆どの石は自然石ではなく、 「 人工石灰岩 ＝ 古代コンクリート 」 である ピラミッドの大方を形成してる石灰岩巨石は、近くに採石場が存在する為に切り出されたそのままの石と思われてるものの、実際にはそうではなく、その詳細な組成分析から 「 人工石灰岩 ＝ 古代コンクリート ＝ ジオポリマー 」 であることが、フランスの ジョセフ・ダヴィドヴィッツ 博士の研究で既に判明してる。 　( その説のかなり詳しい Cottage Window 氏の日本語解説がこちら　http://blog.livedoor.jp/enessay/archives/6658326.html　にある。 　　また ダヴィドヴィッツ 博士自身が海外の別番組で、エジプト古代コンクリート製造再現実験をして見せ、実際に僅か ４ 時間程で巨大な石が固化し、粗削りにも滑らかにも自在に造れるその手順を紹介してる番組も、こちら　https://vimeo.com/1657432　で見られる。 ) 　( 古代コンクリートは巨大な石でも僅か数時間で固まり、現代のコンクリートより遥かに耐久性も高く、ピラミッドの他、ローマの水道橋やコロッセウムもまたそれで造られてる。 ) ● ピラミッドの石はソリと潤滑油ではなく 　　「 クレードルで巻いて、ロープで引いて転がして 」 運び上げられた ピラミッドの石の運び上げに 「 ソリが使われた 」 という説は、ウーダン説でもそのまま採用されていて、４ 度勾配の斜路に造られた溝に油を敷いてソリを滑らせた …と説明されている。 上の画像はウーダン氏と DASSAULT SYSTEMS の製作映像からの引用である。 が、既にクレードルと呼ばれる木製の道具 ( 装着車輪化部材 ) が出土しており、これを巨石の回りに８つ１組で巻き付ければ巨石をそのまま両車輪の如く転がして運べる …というイギリスのディック・パリー教授の仮説が既に存在している。 　　　　 更に、建設大手の大林組は、かなり急勾配の仮設斜路でこの仮説の実証実験 ( 右上の図 ) を行い、成功している。 これらの事実を踏まえて、最終結論となった自説 「 外壁斜面切り通し螺旋斜路 」 ＋ 「 クレードルと足の生えた錘 ( 人間の体重 ) と循環型縄梯子ヤグラの徹底的な活用 」 ＋ 「 石灰岩 ＝ 古代コンクリート 」 説、各々の要点を説明する。 ● 「 内部トンネル型らせん斜路 」 ではなく 「 外壁斜面切り通し螺旋斜路 」 が妥当な理由 「 らせん斜路 」 は、それがピラミッドの構造内に 「 無駄なく組み込まれる 」 為には、ピラミッドの 「 内部 ・内側 」 に造られるしかない。 　　 が、それをワザワザ 「 トンネル型 」 で造る場合の困難さ、マイナス点の多さ、プラス点が殆ど無いこと、については改めて土台から考え直す必要があった。 「 トンネル型 」 で造る場合、高さ ５ メートルにもなるその持ち送り天井が ( 少なくとも急傾斜 「 ５１ 度 ５２ 分 」 の外壁斜面と接しない ) ギリギリ内側より奥の位置に、巾 ２.２ メートルのトンネルを形成するしかない …という理屈になる。 …とすると、その実際の位置は斜路床と同じ高さの外壁斜面からだと、凡そ ６ メートルも内側 ( 下右のウーダン氏の説明図でだとトンネルの中心は ９ メートルも内側 ) 、という計算になる。 　　　　 これらの画像はウーダン氏と DASSAULT SYSTEMS の製作映像からの引用である。 つまり斜路の直ぐ横の外壁の厚さは、４ 〜 ５ メートル ( ウーダン氏の説明図でだと ６ 〜 ８ メートル ) もある …ということになるが、これ程の 「 壁の厚さ 」 はどう見ても非現実的に思えて来る。 そんなにも外壁が厚くて斜路の床位置が奥深かったなら、その斜路床のたった ４ 度の勾配を現在のピラミッドの 「 外壁斜面に残る微かな痕跡から読み取れる 」 なんて事は、絶対に起こりようがない筈なのである。 　[ ウーダン氏はその痕跡を ( 所々に下り階段のある ) 建設作業員 回送用 水平テラス ( 上の図の白い水平部分 ) の全体的な痕跡 と見做してる様であるが、そのようなテラスは外装化粧石の直上には造りようがなく、もっと内側にしか造れなかった筈であることに注意しなければならない。 ] 　　　　 これらの画像はウーダン氏と DASSAULT SYSTEMS の製作映像からの引用である。 さて 「 持ち送り天井 」 の形成は、通常の石積みより遥かに複雑で、極めて慎重な石積み技術が要求される。 　　　　　 が、そうやって苦労して漸く完成するこの斜路部分の 「 持ち送り天井 」 は、その直上の外壁斜面の恐らく ３ 〜 ４ 個の石を支える以外には、唯の 「 陽よけ 」 にしかならないのである。 　( その位置よりもピラミッドの中心に近い 「 外壁斜面上の巨石 」 …の重さは全部、その真下に位置する石組みにと掛かってるだけなので、持ち送り天井が支えてるワケではない。 ) 一体何の為に、そんなにも苦労して斜路に 「 持ち送り天井 」 を形成する必要があるのだろう？ それならばむしろ 「 天井と外壁は無い 」 ものの、その代わりに最も外壁斜面ギリギリに造れる、云わば極限的 「 内部斜路 」 の一種でもある 「 外壁斜面切り通し螺旋斜路 」 だったという見方の方が遥かに妥当性が高い …と気付くではないか？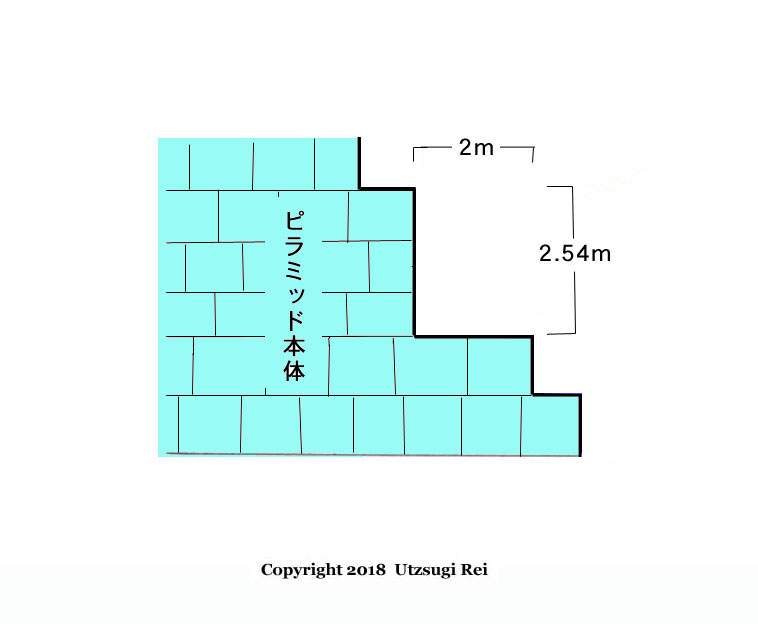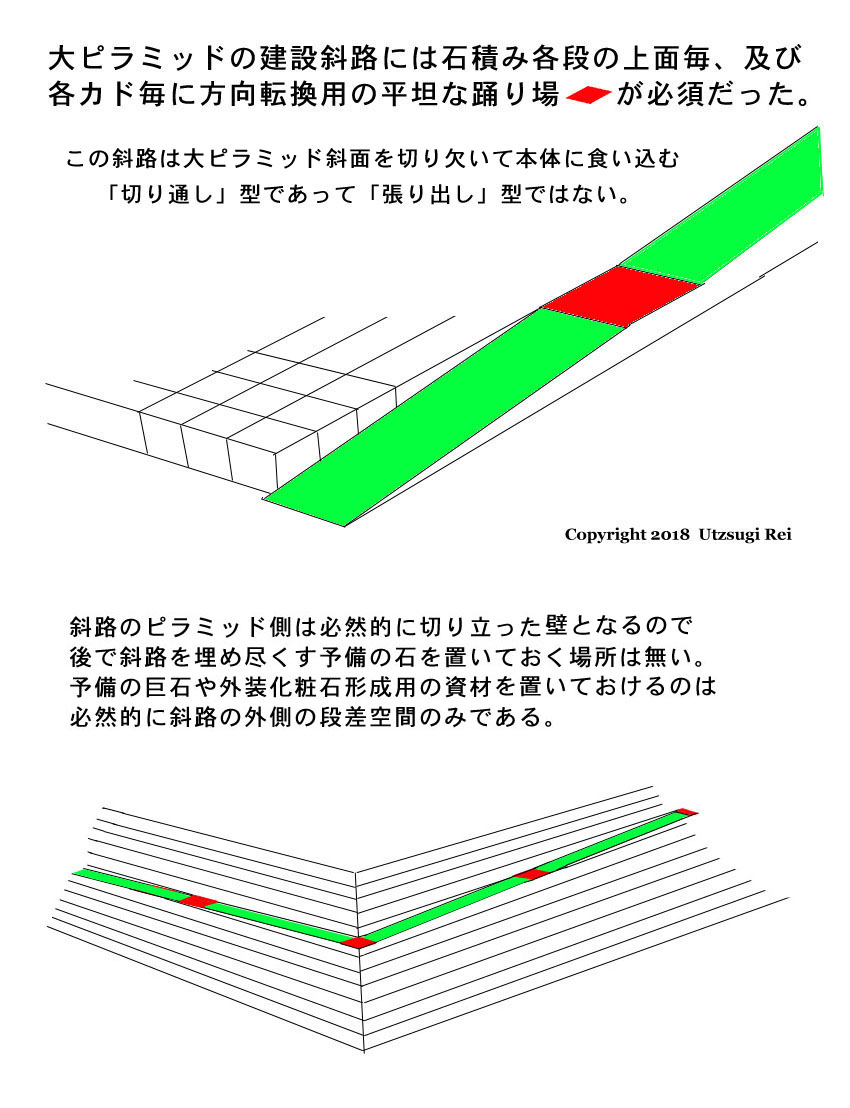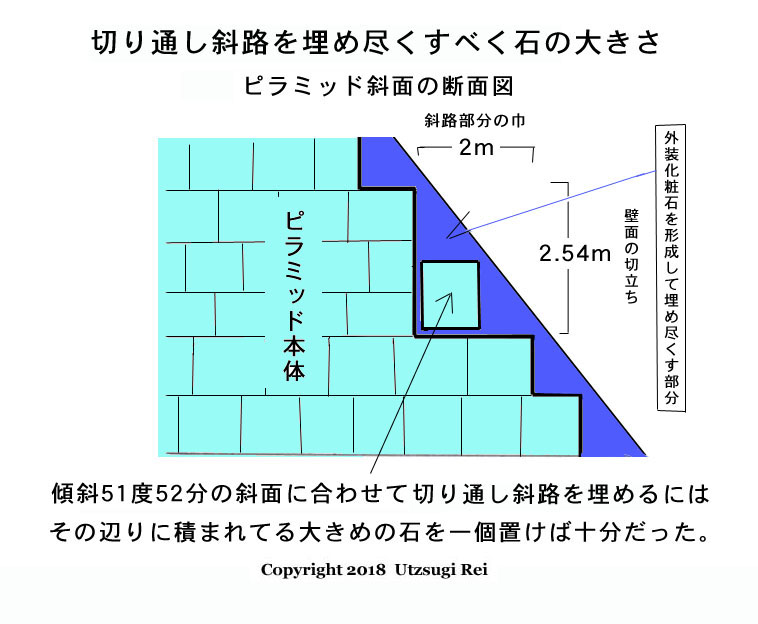 　　　　　　 外壁斜面ギリギリの石積みを、大きな石 １ 個だけ積み残し、勾配 ４ 度で形成される 「 切り通し 」 式の 「 半分内部 ・半分外部の斜路 」 であれば、その形成中と活用中は、最後の外装化粧石の貼り付け ( 形成 ) まで、ピラミッド斜面は今と同じくずっと安全な段々状態である。 　( 外装化粧石の形成は、頂点にキャップストーンが設置されて全方向からの正確な測量が可能になるまでは、実は始めようが無い。 なので、どうしても建造のいちばん最後の段階で、頂点から始めて下へ下へと進めてゆく以外に無かった …と既に分かっている。 より詳しくは本論ページの方に。 ) 　　　　　　 故に、ピラミッドの斜面や斜路からの転落事故の可能性は、実際には殆ど無かった筈である。 また 「 外壁斜面切り通し螺旋斜路 」 であればこそ、その斜路床の勾配の微かな痕跡が、外装を剥ぎ取られて剥き出しの現在のピラミッドの斜面からも読み取れる …という事ではないだろうか？ ● 「 クレードル 」 と 「 足の生えた錘 ( 人間の体重 ) 」 と 「 循環型縄梯子ヤグラ 」 の徹底的な活用 巨石をソリに載せ、ソリの刃を油を敷いたソリ用の溝に嵌め込んで滑らかに滑らせて運び上げる …という方法には、幾つかの重大な欠点がある。 一つは長期に渡る重量物の運搬によって、ソリ溝そのものにヒビが入ったり破損したりは必ず起こって、其処から油がジワジワと滲み出すのを防ぎようが無いこと。 また空のソリの回送路が別に無いなら、頑丈な油まみれの重いソリの回送は、必ず同様なトラブルを斜路の全体に撒き散らしかねないこと。 そしてまた運び上げ作業員自身や、真夜中に斜路内に迷い込んで来る大きな昆虫やヘビや小動物などが、間違ってソリ溝に足を突っ込んだり落ちたりしてまた這い上がって来たりすると、結局長期間の内には ( ソリ溝の中だけでなく ) 斜路の全体、遂にはピラミッドの内部全体までもが、はみ出したり染み出したりした油によって、正に 「 油漬けの状態 」 となってしまうのを、恐らくどうやっても防ぎようが無かったことである。 更にもう一つは、もしも何かの事故が起きて巨石を載せたソリが斜路内を滑り落ち始めた場合、それを簡単に安全に止めることが難しいことである。 何にせよ、ピラミッドの内部全体を油漬けにしてしまいかねないソリ溝と油とが、長年に渡って延々と続いた巨石の運び上げに使われていた可能性は殆ど無い …と考えざる得ない。 実は、これらの問題の完全な解決方法に関しては実際の出土品の中に大きなヒントがあって、それこそが ( 当初はその用途が不明だった ) 下の 「 クレードル 」 なのである。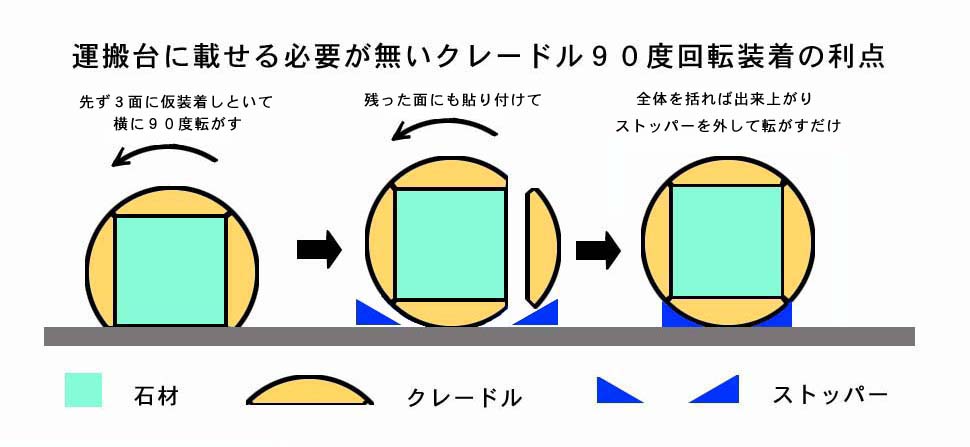 イギリスのディック・パリー教授によってその用途が漸く判明したクレードルは、云わば 「 装着型 車輪化 部材 」 とでも呼ぶべき代物で、これを ８ つ一組にして横倒しにした巨石の両端の周りに先ず ３ つずつ仮固定し、次に ９０ 度だけ転がして残りの面の両端にも １ つずつ張り付け、全体をロープでシッカリと固定し直すと、巨石はその長径を軸とする両輪付きの 「 簡単に転がせる云わば運搬台上の物体 」 に変わるのである。 この方式の極めて優れてる点の一つは、巨石をこの運搬台上に載せるのに唯一度、滑らかに ９０ 度転がすだけで良い点である。 ( その為、台に乗せ上げるという作業が要らない。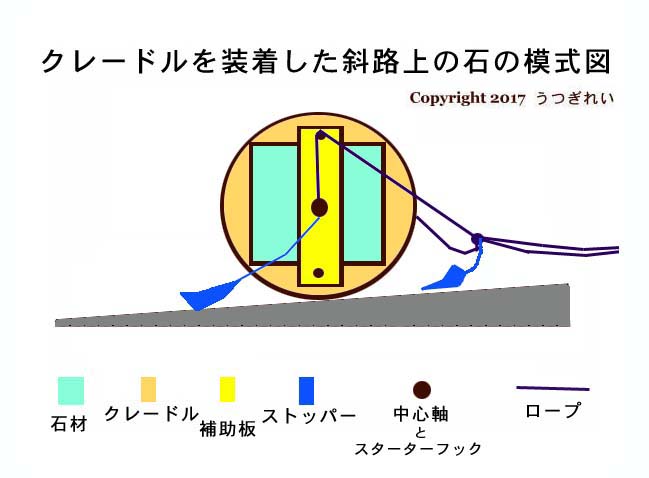 ) またその全体が勝手に転がり出すのを止めるには、その軸両端の中心位置から転がり出し易い側 ( 斜路上では当然下側 ) に細いロープを延ばし、その先に断面が ３ 角形になるストッパーを取り付けておき、そのストッパーを後方に絶えず引き摺りつつ全体が転がるようにしておけば十分である。 ソレは勝手に転がり落ち始めた途端にストッパーが挟まって、巨石は直ぐその場で止まるからである。 　　　　　　　　 クレードルの実用性の実証実験は、建設大手の大林組が既に行っており、その現実的有用性が確認されている。 ( 但し、極めてテレビ的な演出の元で行われたらしい、その実験での斜路勾配は、見ての通り、現実的な ４ 度を遥かに越える　過酷なモノであった。 ) 　　　　　　 ● 最も有用な 「 バランス錘 」 、更には 「 巨石運び上げ動力用 過剰バランス錘 」 として最も効率的かつ効果的な 「 足の生えた錘 」 だった 「 ピラミッド建設の錘役作業員 」 クレードルを巻き付けた巨石と斜路上で対峙 ・拮抗するバランス錘としてだけでなく、それを超える過剰なバランス ( つまり巨石側が力負けして斜路を上らざる得ない状態 ) を実現する力としては、「 労苦を強いる人間の腕力や体力 」 よりも、「 人間の体重そのもの 」 を活用して、それが命令一つで 「 瞬時に特定の或る場所に集中したり、分散したり、移動したり 」 もが自由自在に出来る、最も効率的で効果的な 「 足の生えた、ちゃんと言うことを聞く、生きた錘 」 である …と捉え直すと、その足付きの錘が実現可能な実際的効果は凄まじいもの …ということが判って来る。 こんなにも便利な錘は 「 断じて他に無い 」 のである。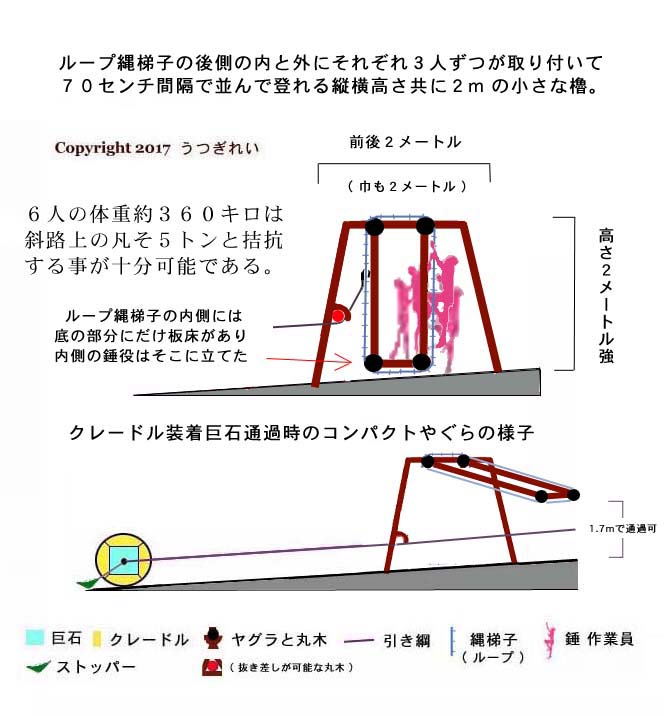 そして僅かに ４ 度勾配の緩やかな斜路上では、垂直に掛かる錘役作業員の体重には、約 １４ 倍ものレバレッジ ( 梃子倍率 ) が掛かるのだ。 だからホンの ３ 人分の体重 １８０ ｋｇ は、クレードルで巻かれて斜路上にある ２.５ トンの巨石と釣り合い、４ 人目、５ 人目では正に楽々、巨石が斜路を上り始めるのである。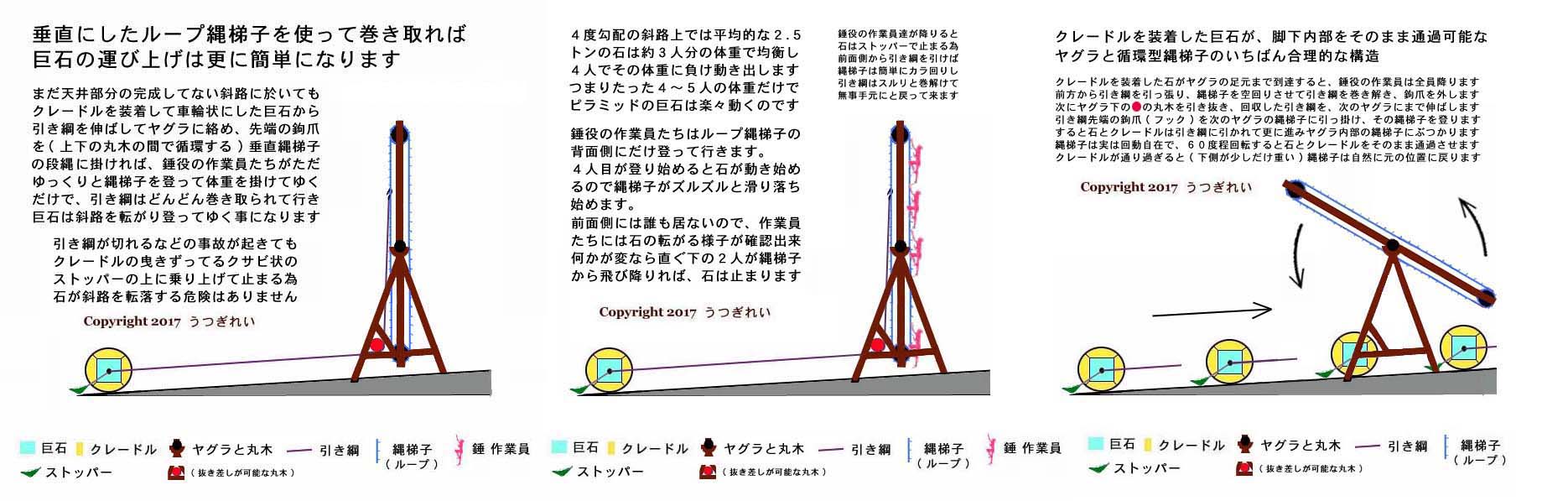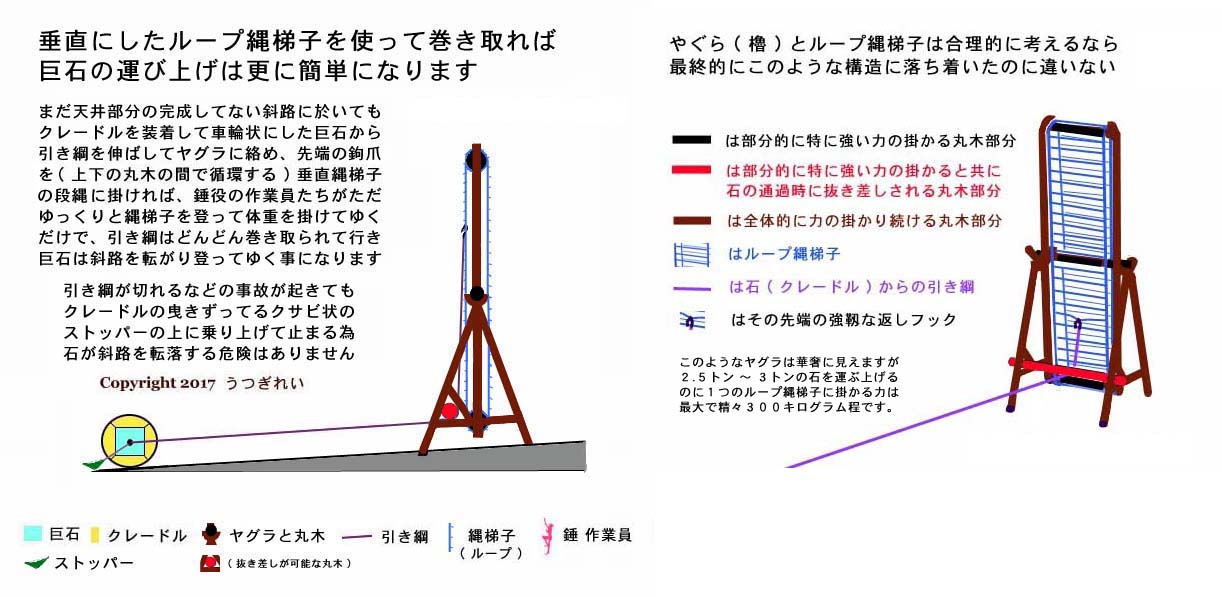 唯一の課題は 「 如何にして錘役作業員の体重を垂直にのみ掛け続けられるか？ 」 だが、これは装着したクレードルの中心位置から延ばした引き綱 ( ナツメヤシのロープ ) を、少なくとも高さ ２ 〜 ５ メートル程のヤグラに張った回動自在の循環型ナワバシゴの段縄と結んでやれば、そのナワバシゴに錘役作業員が取り付いて登ると、その垂直に掛かった体重はそのまま引き綱に伝わる。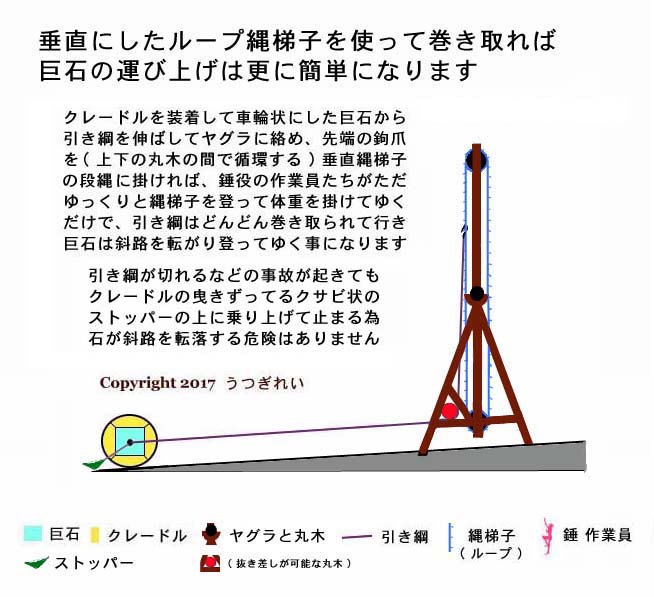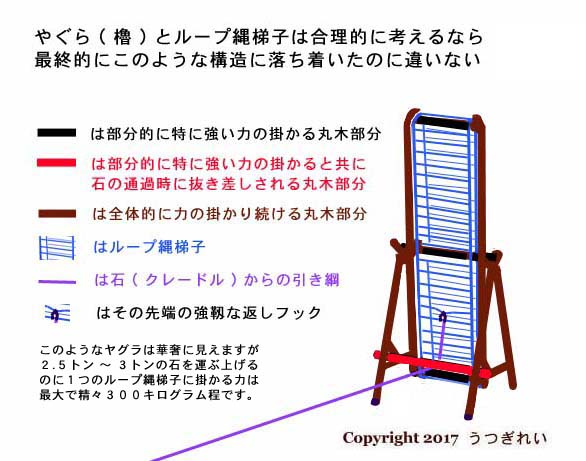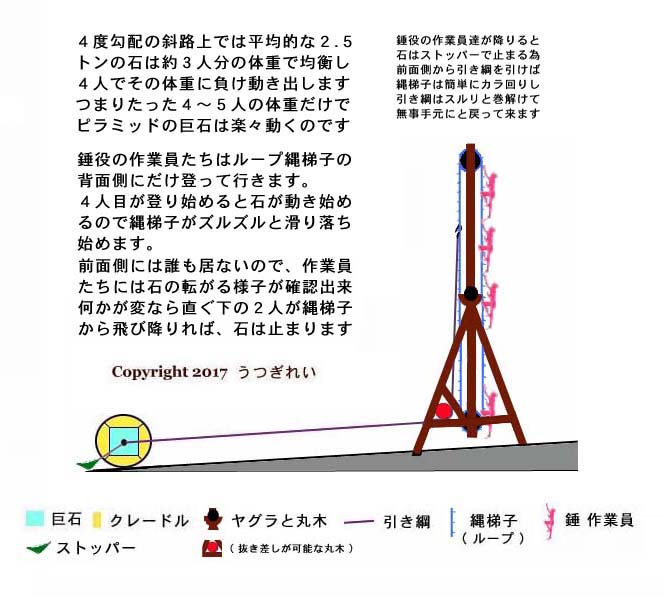 　　　　　　　　 　　　　　　 何人目かが取り付いて登り始めると石が転がり始め、その転がった分だけナワバシゴもズリ下がって来るので、錘役作業員が更に登り続けることで垂直方向に体重を掛け続けられる。 錘役作業員がズリ落ちるナワバシゴを登った分だけ、ナワバシゴは引き綱を巻き取って行き、最小サイズのヤグラの例でだと、ナワバシゴが １ 周する毎に巨石は斜路上を約 ７ メートルほど進み、ヤグラに近付いて来る。 ナワバシゴがズリ落ちて来て、錘役作業員がそれに合わせてナワバシゴを登ってさえいれば ( つまり錘役作業員の足先が床面に着いていなければ ) 、錘役作業員の体重は垂直にナワバシゴにと掛かり続けてることになる。 但し、引き綱がナワバシゴに何周も巻き付くと、引き綱がナワバシゴの全周を強い力で絞め付け始めるので、ナワバシゴがその絞め付け圧で次第に回動しにくくなり、錘役作業員の体重効果が減じる可能性が十分にある。 が、クレードルのストッパーのお陰で、引き綱の張力は何時でも簡単に緩めることが出来、改めて掛け直す事も可能なので、この問題は致命的な困難ではない。 　( この難問についての、もっとより良い解決方法は、何れまた改めて考えてみる事にしたい。) 今にして思えば、この錘役作業員の体重の活用 …というのは、ウーダン説の 「 大回廊上のバランス錘仮説 」 にもそのまま使えたアイディアだったろう。 これらの画像はウーダン氏と DASSAULT SYSTEMS の製作映像からの引用である。 つまり、花崗岩巨石を載せる巨石運搬台とバランス錘の双方共を、最初から 「 頑丈な空のソリ 」 として設定しておくだけで良かった筈 …なのである。 巨石運搬台に花崗岩巨石を載せた後で、大回廊上端位置にある 「 空のソリ 」 上に過剰バランスを成立させられる数の錘役作業員が乗り込むだけで ( 全く体力を使わずにその総体重の凌駕度のみに依って / ２６ 度の大回廊の傾斜ではレバレッヂは掛かりようもなく、むしろマイナスだろうが ) 花崗岩巨石は目的の高さにまでラクラク運び上げられて運搬台から下ろされもしたろう。 錘役作業員の方は大回廊の下の位置にまで辿り着いたソリから降り、そのまま歩いて大回廊の上にまで登り、今度は空っぽになった巨石運搬台の方に乗り込み、大回廊の下に居る 「 空っぽのソリ 」 を上の位置にまで戻しつつ、巨石運搬台を地上の定位置へと降ろしてゆくのである。 或いはもっと合理的に、予め 「 巨石運搬台 」 の方を 「 大回廊上のソリ 」 より重く作っておき、錘役作業員の全員が大回廊の下端で ( ロックした ) ソリから降り、次にそのロックを解除すると、単に巨石運搬台側の過剰な重さによって、空となった ２ つのソリは自然に元々の定位置にまで戻ってゆく …という仕組みにも十分出来たろう。 が、上にも書いた通り 「 巨石運搬台 」 と 「 大回廊 」 は、殆ど同じ傾斜の故にレバレッジがほぼまるで利かないのである。 実際の花崗岩巨石は、平均値の ６０ トンにとどまらず、最大の巨石は １３５ トンもあるから、この肝心要な場面で ４ 度斜路の利点を全部捨て、レバレッジ ( 梃子 ) 効果を一切活用しない …というのは、信じがたい事のように思えるのである。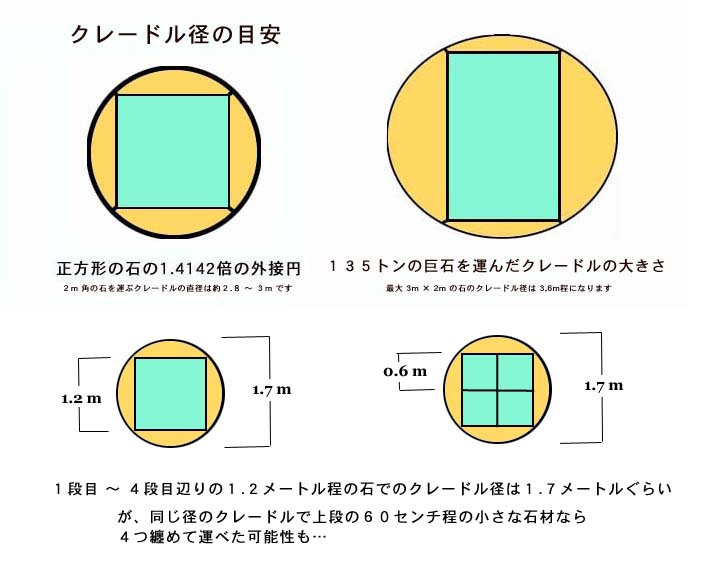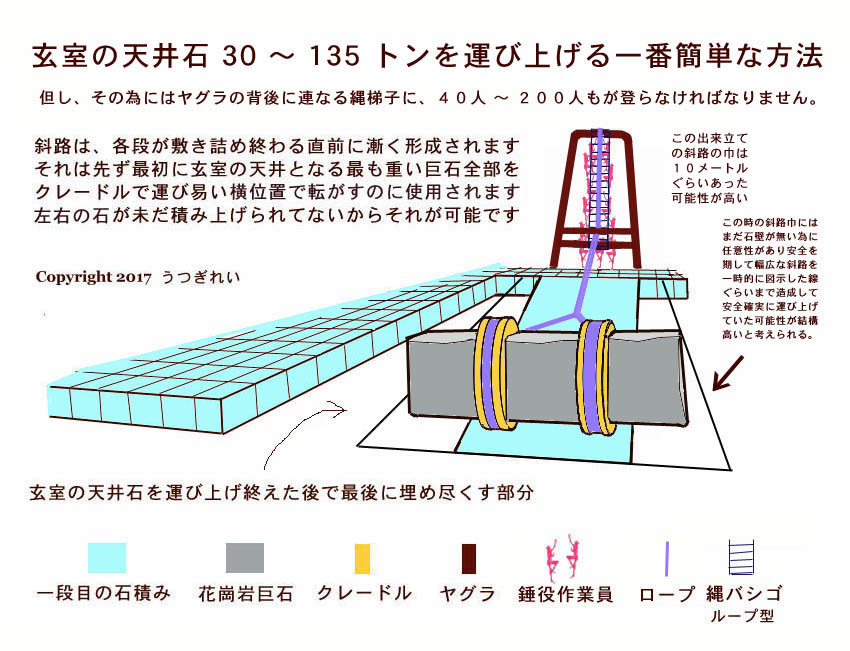 これが玄室天井を覆う １３５ トンの花崗岩巨石である。 …ということで、３０ トン 〜 １３５ トンの花崗岩巨石をも、４ 度斜路の利点をそのまま活かして、最大でも精々 ２００ 人程の体重効果のみで、( 然したる労苦も無しに ) ソレをラクラク運び上げてしまえる方法の説明にと入ろう。 ● 以下は、巨大な花崗岩も横にしてクレードルを巻き付ければ、石が １ 段高く敷き詰められる毎に １４ 〜 ２１ メートル長の仮設斜路を設置して、その上を 強力な クラスター型 ループ ・ラダー ( 連鎖型のループ式ナワ梯子 ) を使ってゴロゴロと転がして行くだけで、総ての巨石はいとも簡単に運び上げが可能だった。 …という、旧説に拘わる考古学者やエジプト学者、そして ジャン・ピエール・ウーダン 氏や クリス・マッシー 氏*までもが正に卒倒しかねない、単純明解なる最終解答である。 　　　　　　 要点； 切り通しでの 「 狭い斜路巾 」 を強いられざる得ないのは、各 建設作業平面が完成した後で 「 地表面から新たに運び上げられる巨石 」 の運搬についてのみであり、各段の建設途中で仮設される斜路には巾を制限される理由などなかった。　( 上左端 と上中右の参考図 を参照されたい。 ) 更にその勾配さえ １ 〜 ４ 度の範囲で自由だった。 [ もしも ２ 度や １ 度だとレバレッヂは ２８ 倍 〜 ５６ 倍も掛かるから、錘役作業員の数はさらに ２ 分の １ ( 最大 １３５ トンの石で １００ 人 ) 、４ 分の １ ( 同じく ５０ 人 ) で済んだろう。 但し ４ 度なら １ 段あたり １４ 〜 ２１ メートルで済む仮設斜路は、２ 度だと ２８ 〜 ４２ メートル、１ 度勾配なら ５６ 〜 ８４ メートルの長さとなる。 巨大な花崗岩巨石が全部設置され終わる高さでの建設台地の広さ、約 １２０ メートル四方から考えたとしても、そのどの勾配でもが十分に採択可能だった筈である。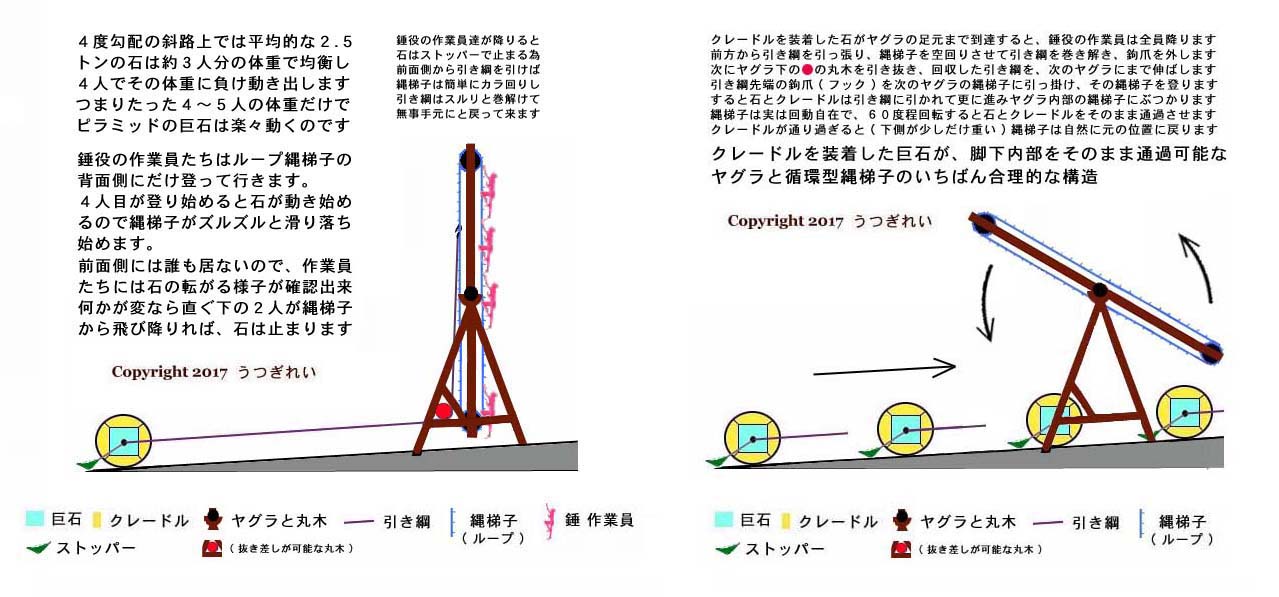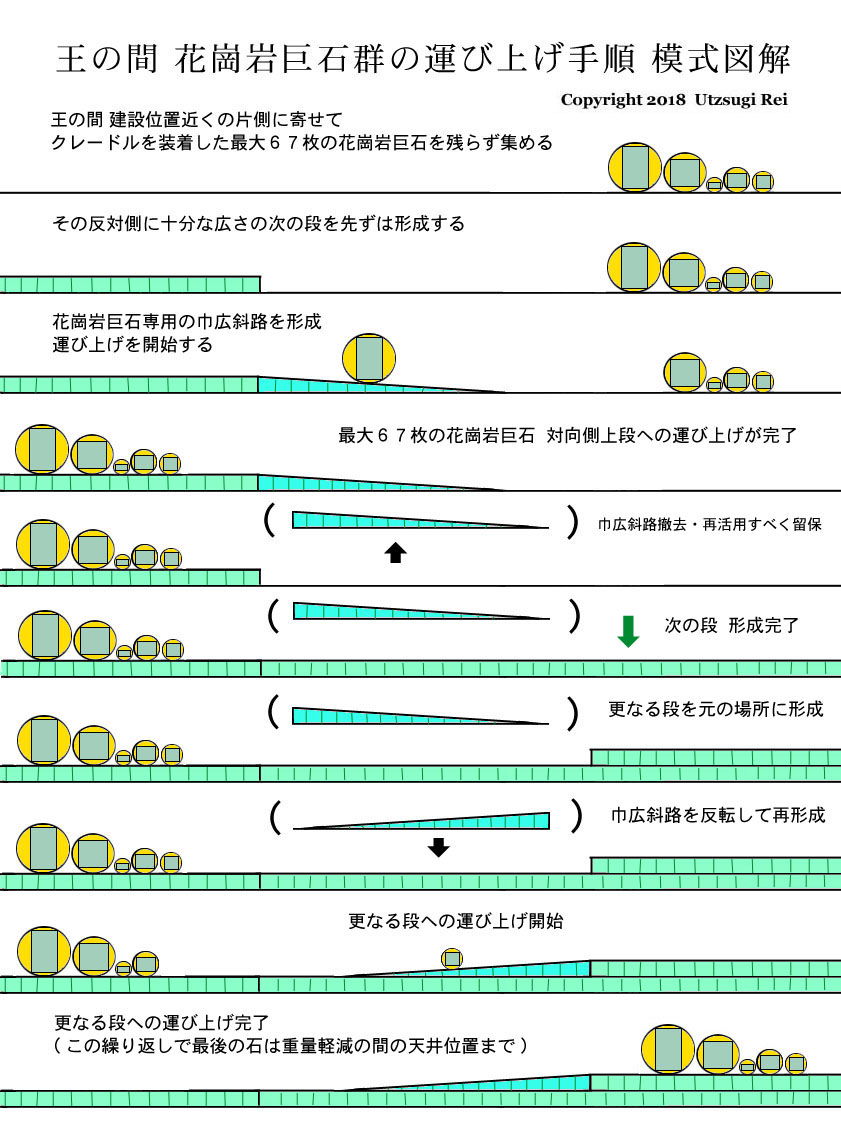 ] 手順； 先ずは、最も重くて大きい ３０ トン 〜 １３５ トンの花崗岩巨石を全部、建設開始までに予め用意しておき、クレードルを装着した状態でストッパーをかませ、絶好の位置に固定しておく。　( 以下、上右端の解説図 を参照されたい。 ) 次に、( あたかも立体プリンターで形成されるかの如く ) 石灰岩巨石が１ 段ずつ積み上がって行き、その段が完成する直前の時点で、巾 １０ メートル程の ４ 度勾配 ( あるいは １ 度 〜 ４ 度勾配 ) の仮設斜路を設置する。 　[ 各段に使用される石の大きさ次第の段差如何によって、この巾広 仮設斜路の凡その長さは １４ ｍ 〜 ２１ ｍ ( あるいは １４ ｍ 〜 ８４ ｍ ) 程のモノである。 但し、この 仮設斜路 は繰り返し使用される。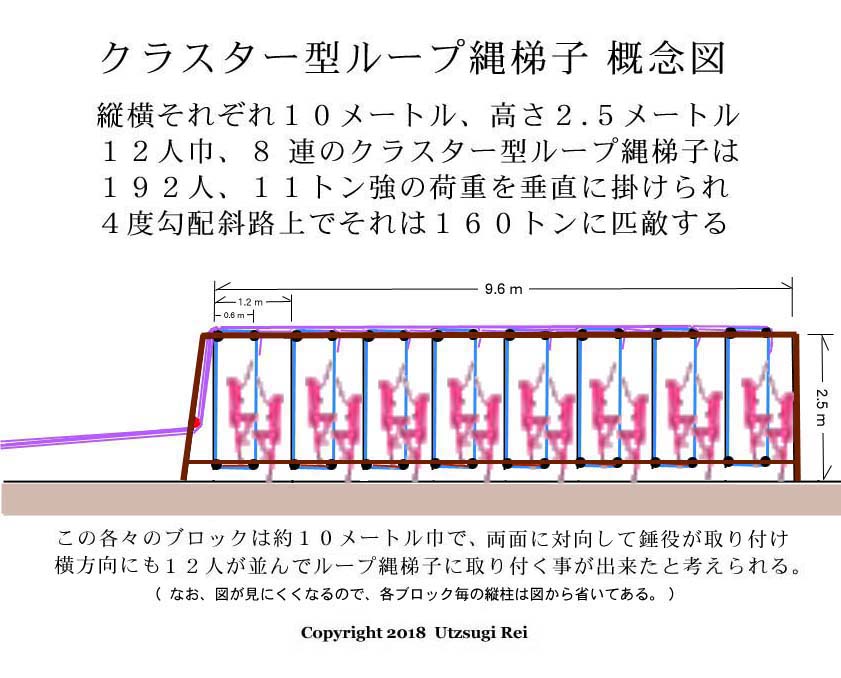] そして次段の上の最奥位置に、クラスター型 ( 連鎖型 ) の 「 ループ・ラダー ( 縄梯子 ) を備える巻き上げヤグラ 」 を設置し、最大 ２００ 人程 ( あるいは最大 ５０ 人 〜 ２００ 人程 ) の錘役作業員がソレに取り付き、垂直に約 １２ トン ( あるいは約 ３ トン 〜 １２ トン ) の体重を掛けられるようにする。　( 上左端 と上中左の参考図 を参照されたい。 ) するとそれは ( 勾配 １ 度 〜 ４ 度の ) 斜路上に在る、最大で約 １６８ トンまでの重量 ( 巨石 ＋ クレードル ＋ ロープの重さ ＋ 摩擦抵抗など ) と拮抗可能な力となり、最大の巨石 １３５ トンをも楽々と転がせるのである。 錘役作業員は特に労苦を伴うこともなく、ただゆっくりと歩調を揃えてループ梯子を登って行くだけで、最大 １３５ トンの花崗岩巨石をも楽々、一段上の段へと運び上げられる。 このやり方を順次繰り返して行く事により、４３ 枚 〜 ６７ 枚の花崗岩巨石の全体が、玄室天井位置である高さ ６０ メートルにまで、運び上げられ得るのである。 ● ピラミッドの大部分を形成してる石灰岩は天然の石灰岩ではなく古代コンクリートだった ピラミッドの大部分を形成してる石灰岩は、天然の石灰岩をその形に切り出したモノではなく、採石場で削り出した石灰岩の粉に砂や砂利、貝殻の破片、動物の骨を砕いた欠片、更に ( 外装化粧石にはそれを白く輝かせる為に ) 多量のオパールの粉までを混ぜ、水を加えて捏ね、砂漠の太陽熱で乾かして固めた古代コンクリート ＝ ジオポリマーであった。 　( オパールの粉が大量に混ざった石灰岩は、自然には存在していないので、ビラミッドの石の殆どが人工石灰岩のブロックで造られてることは決定的である。 ) 　　　　　　　　　　　　 従って後世にピラミッドの表面から剥ぎ取られ、カフラ王ピラミッドの頂上部以外には殆ど残ってない 「 外装化粧石 」 や 「 キャップストーン ( 頂上石 ) 」 の類いは、その形に整形された巨大な石が其処にまで運び上げられてピッタリと嵌め込まれたワケではなく、その場所でこそ 「 形成されたモノ 」 と考えるべきである。 追記 注 * ； クリス・マッシー氏の提唱する ウォーターシャフト仮説 について 水の柱で巨石を １ つ浮上させる毎に当の巨石と同じ重さ以上の水量を建設平面から流さざるを得ず、それを絶えず補充し続けざるを得ず、また最大で ９メートルの巨石を水中でシャフトに収め、浮上させて、建設台地上で取り出す方法が具体的には何処にも見当たらず、更に、巨大な容積を持つシャフトの内壁全体と水門部分での 「 完全な水密性と気密性 」 の確保と維持とが、極めて困難 …どころか、当時使える資材と補修力ではほぼ完全に不可能であること …に恐らく全く思い至っていないらしい、英国人クリス・マッシー氏の提唱する ウォーターシャフト仮説 については、何れまた改めて詳論するつもりである。 ただ当時のエジプトにプラスチック管の気密性に匹敵する素材は無く、巨石を挿入出来る口径での水密および気密を確保可能な水門の扉は入手不可能なのに相違なく、現在でさえ数メートル以上もの直径での完全な気密や水密を確保するのは簡単な事ではないのである。 小さな模型での実験では可能なように見えても、９.８ メートルの高さにまで水の柱が立ち上がる 「 トリチェリーの真空 」 現象を １０ 立方メートルを遥かに越える大きな容積で、しかも古代の石灰岩コンクリートのシャフトでソレを実現するのは、本物の魔法使いでも無ければ恐らく不可能だった …としか思えないのである。 以上 文責　うつぎれい